Heat Flux Measurements and Models

Before the summer of 1950, the only information about sea floor heat flux was 2 measurements of the thermal gradient in deep sea sediments made during the Swedish Albatross expedition (Pettersson, 1949). Refinement of spear-like probes with which to measure temperature gradients, however, marked the beginning of an era of deep sea sediment perforation. With a measurement of the in situ thermal gradient, and laboratory determination of thermal conductivity (from simultaneous cores), the heat flux through a particular sedimented site could be calculated according to Fourier's Law (Ravelle and Maxwell, 1952).

Models of the thermal structure of the lithosphere proliferated as heat flux measurements accumulated and the novel paradigm of plate tectonics became accepted. The observation that heat flux is highest (with isolated intense lows) on the ridge crest and decreases to constant, average heat flux values in older oceanic crust motivated two impressive scientific steps: Elder (1965) suggested that the isolated lows represent recharge zones for submarine hydrothermal systems, 12 years before they were observed; and, a "plate" model in which conductively-cooled crust moved away from a hot boundary at the ridge crest was first used to constrain the nature of mantle convection, and then adapted -- through modifications of boundary conditions applied to the equation of heat transport -- to explain an elegant "1-over-root-t" relationship between the age of oceanic crust and both its bathymetry and heat flux (Parsons & Sclater, 1977).

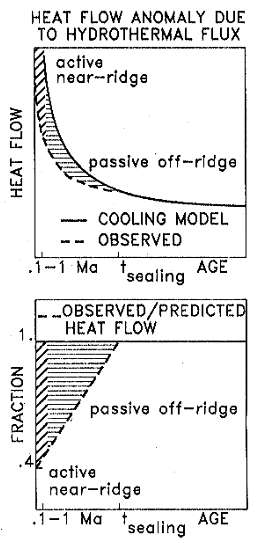It soon became apparent, however, that the conductive plate theory predicted higher heat flux at the ridge crest than was measured. (An interesting question which I've been unable to answer is, "How was conductive heat measured on unsedimented 'fresh' oceanic crust," or "Are heat flux measurments biased towards areas of high sedimentation?") Although the scatter of the near-axis data was high, the difference between prediction and (conductive) measurement was observed in all oceans and dubbed the "heat flux anomaly" in the early 1970's; had plate plate tectonics not been widely accepted at the time, the plate model might have been discarded for its inability to match observation (Anderson, 1986). On the contrary, the magnitude of the heat flux discrepancy was used to estimate the volume of hydrothermal flow, and the anomaly's variation with age utilized to constrain the theoretical partitioning of hydrothermal flux between ridge crest and flank (Stein and Stein, 1994). Thus, it is important to keep in mind that although measurement of convective heat flux has been attempted, the results are few and variable to date; because there may be biases in the conductive data (Stein and Stein, 1994) and inconsistent convective data, the current equation of hydrothermal heat flux with magnitude of the heat flux anomaly warrants substantial skepticism.

From the perspective of organisms in the subsurface seeking habitat, an important constraint derived from heat flux studies is the temperature field. While the temperature field associated with the heat flux predicted by the conductive plate model is relatively simple, the effect of hydrothermal circulation -- where it is possible -- is to deflect the isotherms in proportion to the fluid velocity field. According to the Rayleigh-Darcy criterion, the onset of hydrothermal circulation in the subsurface will depend not only on the vertical thermal gradient, but also the crustal permeability and thickness, the kinematic viscosity of the fluid(s), and the coefficients of thermal conductivity and expansion. Though it is fascinating to consider how organisms in the subsurface might alter fluid properties to their advantage, I will consider the fluid parameters constant at this point. Similarly, thorough modelling of the temperature field will require reconsideration of heat source geometry (and dynamics!), with special attention to the "cracking front" hypothesis of Lister (1974).

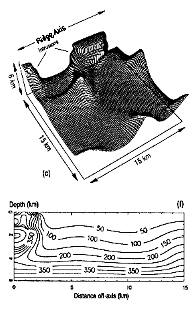Both Travis et al (1991) and Davis et al (1996) provide recent examples of models which account for the deflection of subsurface isotherms by hydrothermal circulation on regional scales. Such approaches are crucial in assessing subsurface habitat at particular sites, for the conductive plate model -- and even a recent revision of it, like the GDH1 (Stein and Stein, 1994) -- involves the averaging of regional data in order to model a general, global relationship between crustal age and heat flux. Assuming a simple, horizontally-layered permeability field (permeability both isotropic and homogeneous within each layer), Travis et al (1991) attempt the first 3-D model of near-axis (<15 km) circulation, successfully investigating the effect of discrete magmatic intrusions along-axis (which is timely given what we have recently deduced about the nature of sea floor spreading through events at the CoAxial segment (1991) and Gorda (1996) ridge). The isothermic surfaces derived from such models offer a unique view of the lower spatial boundary of the habitat available to subsurface organisms; given the temperature at which a particular subsurface organism can survive (or grow optimally), the surface defines how the organism is physically constrained by the temperature field.

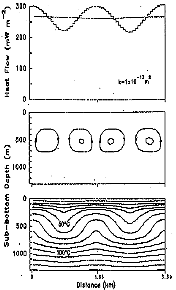Davis et al (1996) devise a similar numerical model to claim that small-scale variations in conductive heat flux measured at the sea floor east of the Endeavour segment are evidence of hydrothermal circulation within ~1 Ma, flat (minimal basement topography) crust beneath about 200 m Cascadia basin sediment. Changing the permeability effects the deflection of the isotherms significantly (click on image to see high-resolution version). Consequently, before attempting to apply heat flux models, and the pursuant temperature field models to habitat definition -- on either the global scale or in a specific region, it is prudent to first discern what is actually known from geology and geophysics about the permeability field in the upper crust.

Outline